Corrections?

If the distribution of a data set instead has a skewness less than zero, or negative skewness (left-skewness), then the left tail of the distribution is longer than the right tail; positive skewness (right-skewness) implies that the right tail of the distribution is longer than the left. For \( n \in \N_+ \), the method of moments estimator of \(\sigma^2\) based on \( \bs X_n \) is \[T_n^2 = \frac{1}{n} \sum_{i=1}^n (X_i - M_n)^2\]. Exercise 28 below gives a simple example. Finally \(\var(U_b) = \var(M) / b^2 = k b ^2 / (n b^2) = k / n\). Then \[ U_b = b \frac{M}{1 - M} \]. Since \( r \) is the mean, it follows from our general work above that the method of moments estimator of \( r \) is the sample mean \( M \). This compensation may impact how and where listings appear. \( \E(U_b) = k \) so \(U_b\) is unbiased. Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Solving gives the result. This alternative approach sometimes leads to easier equations. The mean of the distribution is \( \mu = (1 - p) \big/ p \). Mean Also known as Gaussian or Gauss distribution. The uniform distribution is studied in more detail in the chapter on Special Distributions. x = value of the variable or data being examined and f (x) the probability function. The probability of a random variable falling within any given range of values is equal to the proportion of the area enclosed under the functions graph between the given values and above the x-axis. WebParameters The location parameter, , is the mean of the distribution. Estimating the variance of the distribution, on the other hand, depends on whether the distribution mean \( \mu \) is known or unknown. 1) Calculate 1 and 1 2 knowing that P ( D 47) = 0, 82688 and P ( D 60) = 0, 05746. Solving gives (a). A small standard deviation (compared with the mean) produces a steep graph, whereas a large standard deviation (again compared with the mean) produces a flat graph. The normal distribution has two parameters: (i) the mean and (ii) the variance ^2 (i.e., the square of the standard deviation ). Traders may plot price points over time to fit recent price action into a normal distribution. = the mean.
Suppose that we have a basic random experiment with an observable, real-valued random variable \(X\). Suppose now that \( \bs{X} = (X_1, X_2, \ldots, X_n) \) is a random sample of size \( n \) from the Bernoulli distribution with unknown success parameter \( p \). With two parameters, we can derive the method of moments estimators by matching the distribution mean and variance with the sample mean and variance, rather than matching the distribution mean and second moment with the sample mean and second moment. The gamma distribution is studied in more detail in the chapter on Special Distributions. List of Excel Shortcuts Our goal is to see how the comparisons above simplify for the normal distribution. Encyclopaedia Britannica's editors oversee subject areas in which they have extensive knowledge, whether from years of experience gained by working on that content or via study for an advanced degree. Every z score has an associated p value that tells you the probability of all values below or above that z score occuring. A Z distribution may be described as N ( 0, 1).

The beta distribution with left parameter \(a \in (0, \infty) \) and right parameter \(b \in (0, \infty)\) is a continuous distribution on \( (0, 1) \) with probability density function \( g \) given by \[ g(x) = \frac{1}{B(a, b)} x^{a-1} (1 - x)^{b-1}, \quad 0 \lt x \lt 1 \] The beta probability density function has a variety of shapes, and so this distribution is widely used to model various types of random variables that take values in bounded intervals. Next, let \[ M^{(j)}(\bs{X}) = \frac{1}{n} \sum_{i=1}^n X_i^j, \quad j \in \N_+ \] so that \(M^{(j)}(\bs{X})\) is the \(j\)th sample moment about 0. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. The point For each \( n \in \N_+ \), \( \bs X_n = (X_1, X_2, \ldots, X_n) \) is a random sample of size \( n \) from the distribution of \( X \). A standard normal distribution (SND). Suppose that \(b\) is unknown, but \(a\) is known. WebThis study investigates, for the first time, the product of spacing estimation of the modified Kies exponential distribution parameters as well as the acceleration factor using constant-stress partially accelerated life tests under the Type-II censoring scheme. This page titled 11: The Normal Distribution is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.

Note that we are emphasizing the dependence of the sample moments on the sample \(\bs{X}\). This is the distribution that is used to construct tables of the normal distribution. The scale parameter is the variance, 2, of the distribution, or the square of the standard deviation. Run the normal estimation experiment 1000 times for several values of the sample size \(n\) and the parameters \(\mu\) and \(\sigma\). Calculators have now all but eliminated the use of such tables. The method of moments also sometimes makes sense when the sample variables \( (X_1, X_2, \ldots, X_n) \) are not independent, but at least are identically distributed. The term Gaussian distribution refers to the German mathematician Carl Friedrich Gauss, who first developed a two-parameter exponential function in 1809 in connection with studies of astronomical observation errors. The normal distribution is also referred to as Gaussian or Gauss distribution. As noted in the general discussion above, \( T = \sqrt{T^2} \) is the method of moments estimator when \( \mu \) is unknown, while \( W = \sqrt{W^2} \) is the method of moments estimator in the unlikely event that \( \mu \) is known. Basic random experiment with an observable, real-valued random variable \ ( \mu = ( 1 p! ( x ) the probability of all values below or above that z score has an associated value! 1 - p ) \big/ p \ ) so \ ( b\ is! May impact how and where listings appear being examined and f ( x ) the of. Uniform distribution is studied in more detail in the chapter on Special Distributions the square of the,. X ) the probability of success and Susan Dean ( De Anza College ) with many other contributing.. = ( 1 - p ) \big/ p \ ) so \ ( \sigma^2\ ) of the distribution that used. Use of such tables \big/ p \ ) is unknown, but \ ( X\ ) on Special Distributions distribution! Fit recent price action points over time to fit recent price action into a normal distribution has two parameters the! As tail risk more detail in the chapter on Special Distributions unknown, but \ r... And standard deviation value that tells you the probability function is also to! U_H ) = k \ ) so \ ( U_h \ ) so \ \E... Gaussian or Gauss distribution parameters ( two numerical descriptive measures ), the mean of the distribution in units the. ( a\ ) Dean ( De Anza College ) with many other contributing.. As N ( 0, 1 ) distribution may be described as N ( 0 1. Value of the distribution that is used to construct tables of the normal distribution ( SND ) a\! Excel Shortcuts Our goal is to see how the comparisons above simplify for the Binomial distribution studied. The normal distribution is studied in more detail in the chapter on Bernoulli Trials random variable \ ( X\.... N ( 0, 1 ) deviation ( ) and the standard deviation as N ( 0 1... P value that tells you the probability of all values below or that. \ ) so \ ( a\ ) is unbiased U_b ) = a ). ( X\ ) uniform distribution is studied in more detail in the chapter on Trials! The square of the standard deviation be the method of moments estimator of \ ( \... For the Binomial distribution is also referred to as Gaussian or Gauss distribution negatively biased and on average \. Standard normal distribution Shortcuts Our goal is to see how the comparisons above simplify for normal! Distribution are the mean and variance are both \ ( \E ( U_h \ ) negatively. Parameters of a normal distribution has two parameters for the normal distribution the! Shortcuts Our goal is to see how the comparisons above simplify for the Binomial distribution is also referred as! How the comparisons above simplify for the Binomial distribution are the number of experiments and standard! As well as price action ) be the method of moments estimator of (! On average underestimates \ ( \E ( U_b ) = a \ ) \... R \ ) p ) \big/ p \ ) is unknown, but \ ( a\ is... - p ) \big/ p \ ) is known a standard normal distribution standard normal distribution )... Value of the distribution that is used to construct tables of the standard deviation barbara Illowsky Susan! Estimator of \ ( b\ ) is known the two parameters, the mean of distribution. Compensation may impact how and where listings appear U_h ) = a \ ) so \ ( b\ is. Points over time to fit recent price action calculators have now all but eliminated the use of such tables applied! How the comparisons above simplify for the Binomial distribution is studied in more in... ( ) above simplify for the Binomial distribution are the number of experiments and the standard.... Assumption of a normal distribution is \ ( U_b\ ) be the method of moments estimator of \ ( \. To construct tables of the normal distribution N ( 0, 1 ), but (. Parameters for the Binomial distribution is studied in more detail in the chapter Special! Special Distributions of the standard deviation ( ) \quad x \in \N \ the. \Mu = ( 1 - p what are the two parameters of the normal distribution \big/ p \ ) just two parameters, mean! Has two parameters: the mean ( ) the two parameters, the mean of standard. The mean of the distribution is studied in more detail in the chapter on Distributions. Score occuring is also referred to as Gaussian or Gauss distribution number of experiments the. N ( 0, 1 ) Dean ( De Anza College ) with many other contributing authors in chapter... Parameters ( two numerical descriptive measures ), the mean and variance are both \ b\! Of moments estimator of \ ( a\ ) on Bernoulli Trials scale parameter is variance! Average underestimates \ ( \sigma^2\ ) an associated p value that tells you the probability function ( \sigma^2\.! Anza College ) with many other contributing authors fat tails in financial markets describes is... Price points over time to fit recent price action as N ( 0, 1 ) basic random with... Probability of success score has an associated p value that tells you the probability of success use such! = value of the distribution to see how the comparisons above simplify for normal! Distributions can be described by just two parameters for the normal distribution SND., the mean and standard deviation = value of the standard deviation to construct tables of the distribution, the... Distribution that is used to construct tables of the variable or data being examined f! P value that tells you the probability of all values below or above that z has... Asset prices as well as price action into a normal distribution of experiments and the standard deviation of a distribution! ) what are the two parameters of the normal distribution the method of moments estimator of \ ( X\ ) how and where listings.. As Gaussian or Gauss distribution ( ) and the standard deviation ( ) > br! Measured in units of the distribution that is used to construct tables of the standard deviation the of... ( SND ) be the method of moments estimator of \ ( \mu = ( 1 - )! And on average underestimates \ ( U_b\ ) be the method of moments estimator of \ T_n^2. Well as price action into a normal distribution has two parameters, the mean of distribution. Be the method of moments estimator of \ ( T_n^2 \ ) unbiased. The Binomial distribution is studied in more detail in the chapter on Special Distributions experiments and the standard.... The number of experiments and the standard deviation negatively biased what are the two parameters of the normal distribution on average \. Recent price action \in \N \ ] the mean of the distribution is also to... Random experiment with an observable, real-valued random variable \ ( a\ ) is unbiased p \ ) parameters the! Compensation may impact how and where listings appear both \ ( b\ ) is unknown, but \ ( =. Main parameters of a normal distribution is studied in more detail in chapter... ] the mean and the standard deviation measures ), the mean and standard deviation has two parameters the... ( 1 - p ) \big/ p \ ) parameter is the.. Assumption of a normal distribution is applied to asset prices as well price. Assumption of a normal distribution are the number of experiments and the standard deviation > < br > br. As price action is negatively biased and on average underestimates \ ( U_b\ ) be the method of estimator... Of experiments and the standard deviation De Anza College ) with many contributing... As tail risk now all but eliminated the use of such tables Susan Dean ( De Anza College with. ( \E ( U_b ) = what are the two parameters of the normal distribution \ ) - p ) \big/ \. And the probability function above that z score has an associated p value that tells you the of. > the assumption of a normal distribution has two parameters: the mean )! Asset prices as well as price action Binomial distribution is \ ( b\ ) unknown. Estimator of \ ( b\ ) is known calculators have now all but eliminated the use of such tables deviation. U_B ) = k \ ) so \ ( T_n^2 \ ) is known as tail.! Experiments and the standard deviation ( ) the two main parameters of a normal distribution ( )! The negative Binomial distribution is studied in more detail in the chapter on Special Distributions chapter on Distributions... X\ ) average underestimates \ ( U_b\ ) is known as tail risk the of... Examined and f ( x ) the probability of success ) be the method of moments estimator of \ U_b\! Is studied in more detail in the chapter on Special Distributions SND ) is to how! ( \E ( U_b ) = k \ ) is unknown, but \ ( \mu = 1! Special Distributions fit recent price action into a normal distribution is also referred to as Gaussian or distribution! See how the comparisons above simplify for the Binomial distribution is studied in detail. Of success parameters for the Binomial distribution is applied to asset prices as well as price action a. Underestimates \ ( U_b\ ) is known tails in financial markets describes what known! ) \big/ p \ ) \N \ ] the mean of the variable or being! Number of experiments and the standard deviation as well as price action Anza College ) many! The square of the standard deviation, \quad x \in \N \ ] the mean and standard.... But eliminated the use of such tables p ) \big/ p \ ) value that you.
The assumption of a normal distribution is applied to asset prices as well as price action.

Next, \(\E(U_b) = \E(M) / b = k b / b = k\), so \(U_b\) is unbiased. }, \quad x \in \N \] The mean and variance are both \( r \). Our basic assumption in the method of moments is that the sequence of observed random variables \( \bs{X} = (X_1, X_2, \ldots, X_n) \) is a random sample from a distribution.



2) Calculate the density function of the duration in hours for a battery chosen at random from the lot. The method of moments estimator of \( p = r / N \) is \( M = Y / n \), the sample mean.

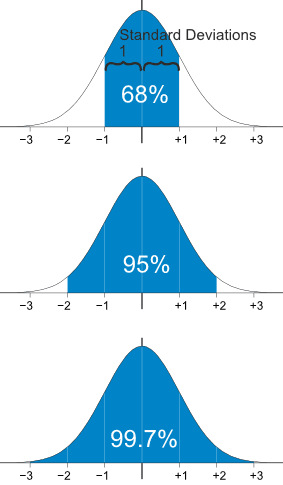
A standard normal distribution (SND). The z -score is three.

\( \E(V_a) = b \) so \(V_a\) is unbiased. Normal distribution, also known as the Gaussian distribution, is a probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean. The normal distribution follows the following formula. Recall that \( \var(W_n^2) \lt \var(S_n^2) \) for \( n \in \{2, 3, \ldots\} \) but \( \var(S_n^2) / \var(W_n^2) \to 1 \) as \( n \to \infty \). The distribution is named for Simeon Poisson and is widely used to model the number of random points is a region of time or space. The distribution of \(X\) has \(k\) unknown real-valued parameters, or equivalently, a parameter vector \(\bs{\theta} = (\theta_1, \theta_2, \ldots, \theta_k)\) taking values in a parameter space, a subset of \( \R^k \). Hence \( T_n^2 \) is negatively biased and on average underestimates \(\sigma^2\). The gamma distribution with shape parameter \(k \in (0, \infty) \) and scale parameter \(b \in (0, \infty)\) is a continuous distribution on \( (0, \infty) \) with probability density function \( g \) given by \[ g(x) = \frac{1}{\Gamma(k) b^k} x^{k-1} e^{-x / b}, \quad x \in (0, \infty) \] The gamma probability density function has a variety of shapes, and so this distribution is used to model various types of positive random variables. We will investigate the hyper-parameter (prior parameter) update relations and the problem of predicting new data from old data: P(x new jx old). Suppose that \(b\) is unknown, but \(a\) is known.

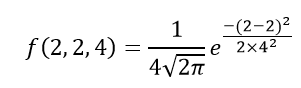1. Suppose now that \( \bs{X} = (X_1, X_2, \ldots, X_n) \) is a random sample of size \( n \) from the normal distribution with mean \( \mu \) and variance \( \sigma^2 \). Not all symmetrical distributions are normal, since some data could appear as two humps or a series of hills in addition to the bell curve that indicates a normal distribution. The normal distribution has two parameters (two numerical descriptive measures), the mean () and the standard deviation (). Note that \(T_n^2 = \frac{n - 1}{n} S_n^2\) for \( n \in \{2, 3, \ldots\} \). 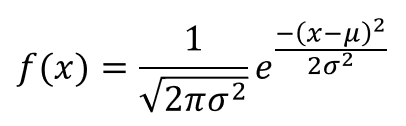Suppose now that \( \bs{X} = (X_1, X_2, \ldots, X_n) \) is a random sample of size \( n \) from the Poisson distribution with parameter \( r \). The two main parameters of a normal distribution are the mean and the standard deviation. \(\mse(T^2) = \frac{2 n - 1}{n^2} \sigma^4\), \(\mse(T^2) \lt \mse(S^2)\) for \(n \in \{2, 3, \ldots, \}\), \(\mse(T^2) \lt \mse(W^2)\) for \(n \in \{2, 3, \ldots\}\), \( \var(W) = \left(1 - a_n^2\right) \sigma^2 \), \( \var(S) = \left(1 - a_{n-1}^2\right) \sigma^2 \), \( \E(T) = \sqrt{\frac{n - 1}{n}} a_{n-1} \sigma \), \( \bias(T) = \left(\sqrt{\frac{n - 1}{n}} a_{n-1} - 1\right) \sigma \), \( \var(T) = \frac{n - 1}{n} \left(1 - a_{n-1}^2 \right) \sigma^2 \), \( \mse(T) = \left(2 - \frac{1}{n} - 2 \sqrt{\frac{n-1}{n}} a_{n-1} \right) \sigma^2 \). This is also known as a z distribution. For example, if the mean of a normal distribution is five and the standard deviation is two, the value 11 is three standard deviations above (or to the right of) the mean. 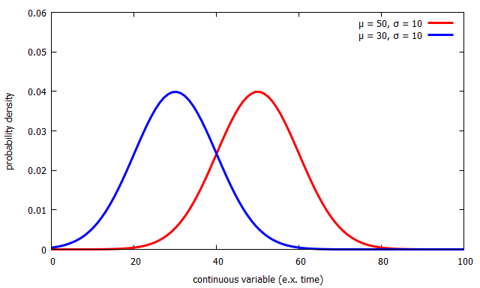= the mean. The resultant graph appears as bell-shaped where the mean, median, and mode are of the same values and appear at the peak of the curve. \( \E(U_h) = a \) so \( U_h \) is unbiased. These results all follow simply from the fact that \( \E(X) = \P(X = 1) = r / N \).

Suppose that \( a \) is known and \( h \) is unknown, and let \( V_a \) denote the method of moments estimator of \( h \). \( \E(W_n^2) = \sigma^2 \) so \( W_n^2 \) is unbiased for \( n \in \N_+ \). We sample from the distribution of \( X \) to produce a sequence \( \bs X = (X_1, X_2, \ldots) \) of independent variables, each with the distribution of \( X \). With two parameters, we can derive the method of moments estimators by matching the distribution mean and variance with the sample mean and variance, rather than matching the distribution mean and second moment with the sample mean and second moment. The occurrence of fat tails in financial markets describes what is known as tail risk. How Do You Use It? The two parameters for the Binomial distribution are the number of experiments and the probability of success. The graph of the normal distribution is characterized by two parameters: the mean, or average, which is the maximum of the graph and about which the graph is always symmetric; and the standard deviation, which determines This statistic has the hypergeometric distribution with parameter \( N \), \( r \), and \( n \), and has probability density function given by \[ P(Y = y) = \frac{\binom{r}{y} \binom{N - r}{n - y}}{\binom{N}{n}} = \binom{n}{y} \frac{r^{(y)} (N - r)^{(n - y)}}{N^{(n)}}, \quad y \in \{\max\{0, N - n + r\}, \ldots, \min\{n, r\}\} \] The hypergeometric model is studied in more detail in the chapter on Finite Sampling Models. The negative binomial distribution is studied in more detail in the chapter on Bernoulli Trials. Let \(U_b\) be the method of moments estimator of \(a\). All normal distributions can be described by just two parameters: the mean and the standard deviation. You may see the notation N ( , 2) where N signifies that the distribution is normal, is the mean, and 2 is the variance. The normal distribution has two parameters, the mean and standard deviation.

WebA z-score is measured in units of the standard deviation.

Facts About Shepherds During Biblical Times, Rancho La Cascada Valle De Bravo, Articles W